Lecture 10
Constructing a Scanner - Quick Review
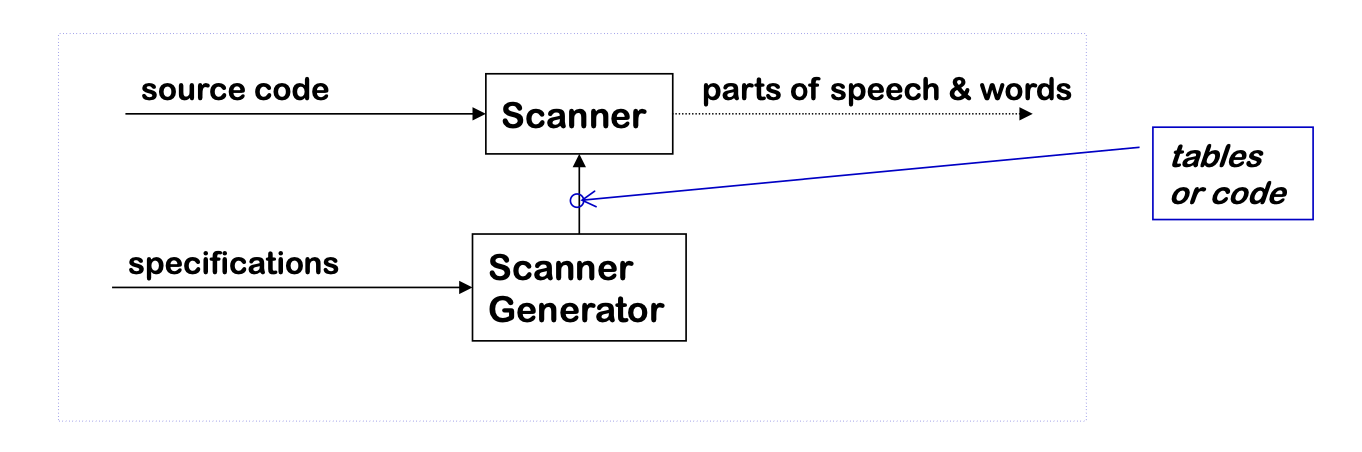
- The scanner is the first stage in the front end
- Specifications can be expressed using regular expressions
- Build tables and code from a DFA
Goal
- We will show how to construct a finite state automata to recognize any RE
- Overview:
- Direct construction of a nondeterministic finite automata (NFA) to recognize a given RE
- Requires ε-transitions to combine regular subexpressions
- Construct a deterministic finite automata (DFA) to simulate the NFA
- Use a set-of-states construction
- Generate the scanner code
- Additional specifications needed for details
- Direct construction of a nondeterministic finite automata (NFA) to recognize a given RE
NFAs
- An NFA accepts a string x iff ∃ a path through the transition graph from s0 to a final state such that the edge labels spell x
- Transitions on ε consume no input
- To “run” the NFA, start in s0 and guess the right transition at each step
- Always guess correctly
- If some sequence of correct guesses accepts x then accept
Why study NFAs?
- They are they key to automating the RE -> DFA construction
- We can paste together NFAs with ε transitions
Relationship between NFAs and DFAs
DFA is a special case of an NFA
- DFA has no ε transitions
- DFA’s transition function is single-valued
- Same rules will work
DFA can be simulated with an NFA
- Obviously
NFA can be simulated with a DFA
- Less obvious
- Simulate sets of possible states
- Possible exponential blowup in the state space
- Still, one state transition per character in the input stream
Automating Scanner Construction
To convert a specification into code:
- Write down the RE for the input language
- Build a big NFA
- Build the DFA that simulates the NFA
- Systematically shrink the DFA
- Turn it into code
Scanner generators
- Lex and Flex work along these lines
- Algorithms are well known and well understood
- Key issue is interface to parser
- You could build one in a weekend!
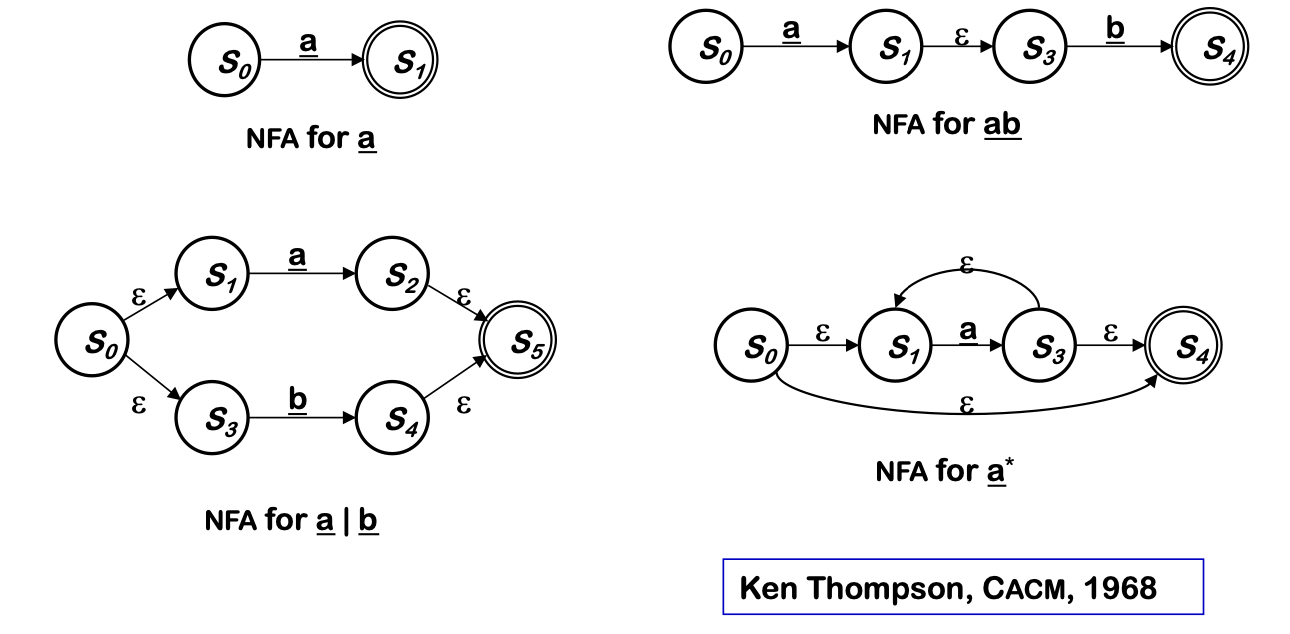
RE -> NFA (Thompson’s construction)
- Build an NFA for each term
- Combine them with ε moves
NFA -> DFA (subset construction)
- Build the simulation
DFA -> Minimal DFA
- Hopcroft’s algorithm
DFA -> RE (Not part of the scanner construction)
- All pairs, all paths problem
- Take the union of all paths from s0 to an accepting state
RE -> NFA using Thomspon’s Construction
Key idea
- NFA pattern for each symbol and each operator
- Each NFA has a single start and accept state
- Join them with ε moves in precedence order
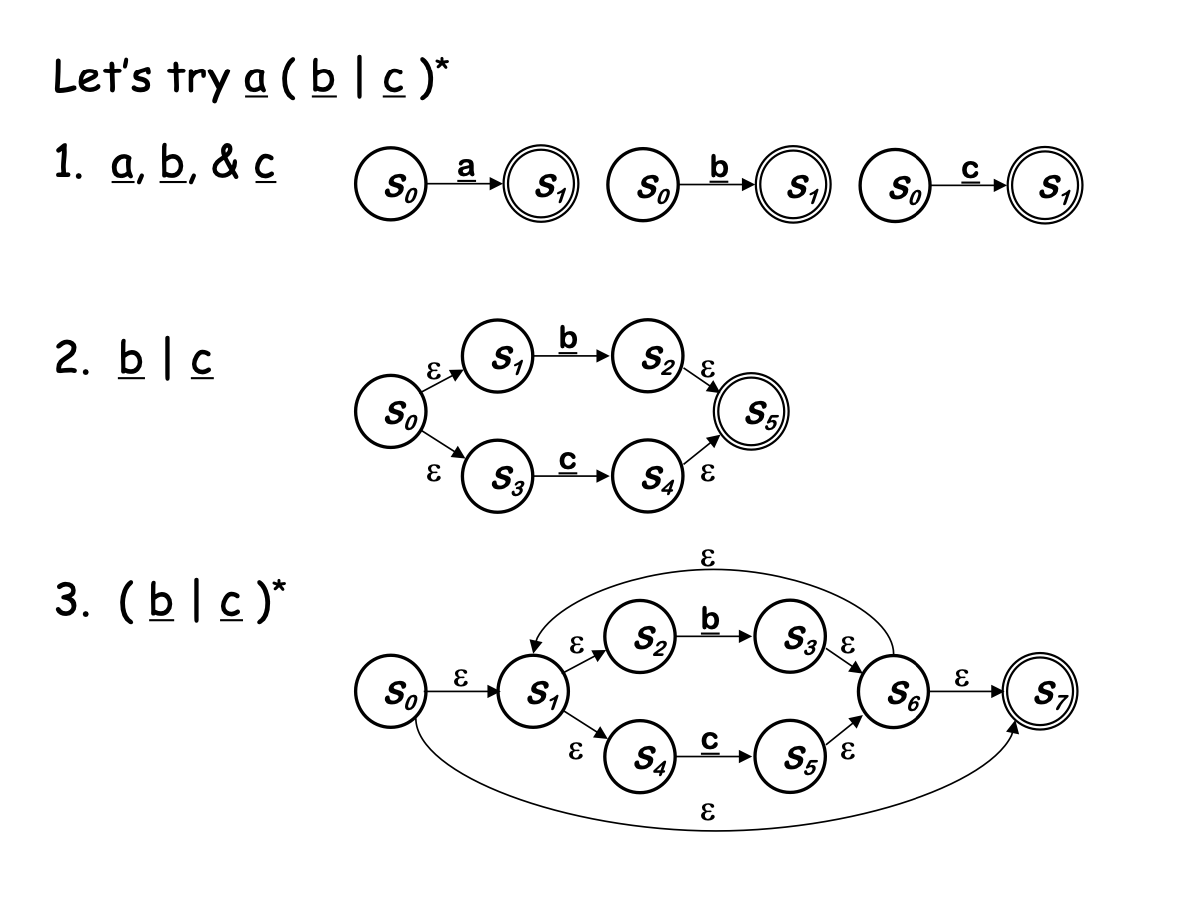
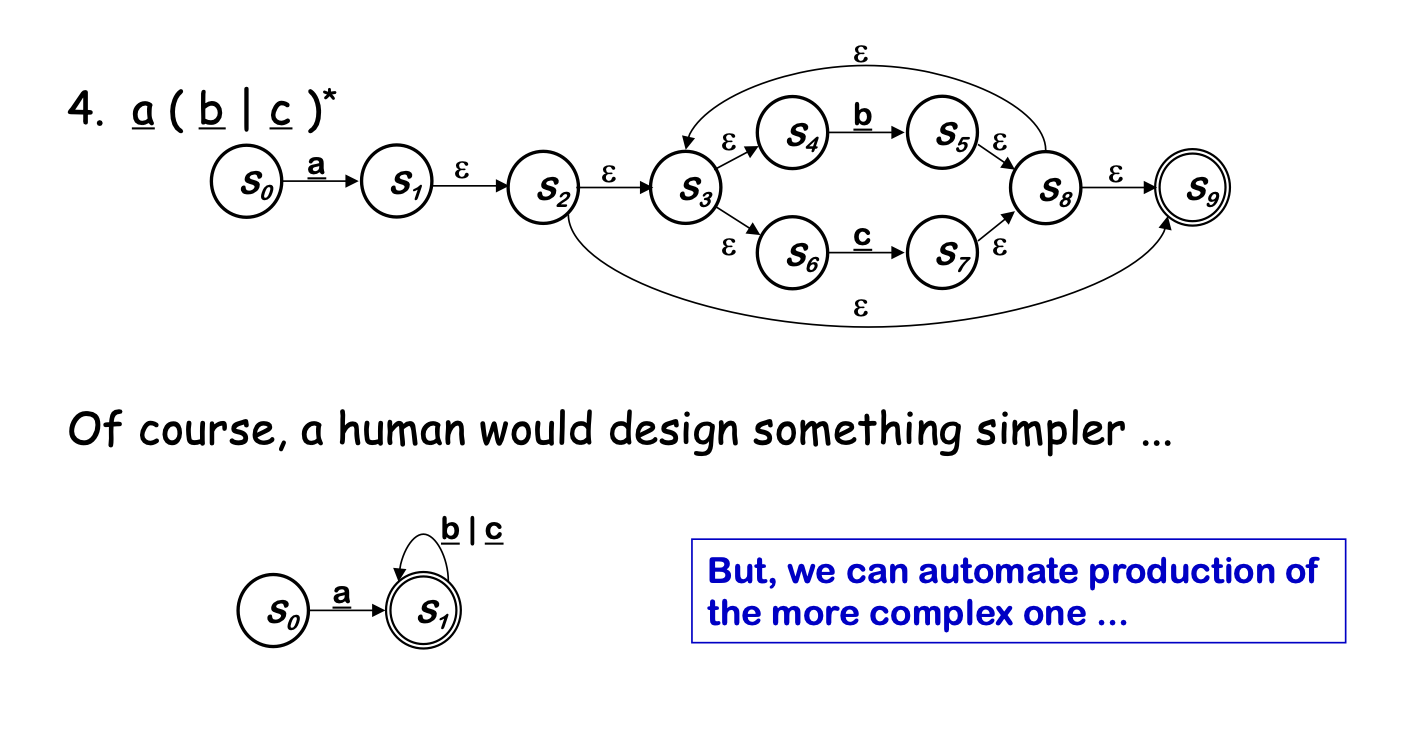
Examples
NFA -> DFA with Subset Construction
Need to build a simulation of the NFA
Two key functions
move(si, a)is a set of states reachable from si by aε-closure(si)is the set of states reachable from si by ε
The algorithm (sketch):
- Start state derived from s0 of the NFA
- Take its
ε-closureS0 =ε-closure(s0) - For each state S, compute
move(S, a)for each a ∈ Σ, and take it’s ε-closure - Iterate until no more states are added
Sounds more complex that it is…
Algorithm:
s0 <- ε-closure(q0)
add s0 to S
while (S is still changing)
for each si ∈ S
for each a ∈ Σ
s? <- ε-closure(move(si, a))
if (s? ∉ S) then
add s? to S as sj
T[si, a] <- sj
else
T[si, a] <- s?The algorithm halts:
- S contains no duplicates (test before adding)
- 2^Q is finite
- while loop adds to S, but does not remove from S (monotone) => the loop halts
S contains all the reachable NFA states
- It tries each symbol in each si
- It builds every possible NFA configuration => S and T form the DFA
Example of a fixed-point computation
- Monotone construction of some finite set
- Halts when it stops adding to the set
- Proofs of halting & correctness are similar
- These computations arise in many contexts
Other fixed-point computations
- Canonical construction of sets of LR(1) items
- Quite similar to the subset construction
- Classic data-flow analysis
- Solving sets of simultaneous set equations
- DFA minimization algorithm (coming up!)
We will see many more fixed-point computations
Example
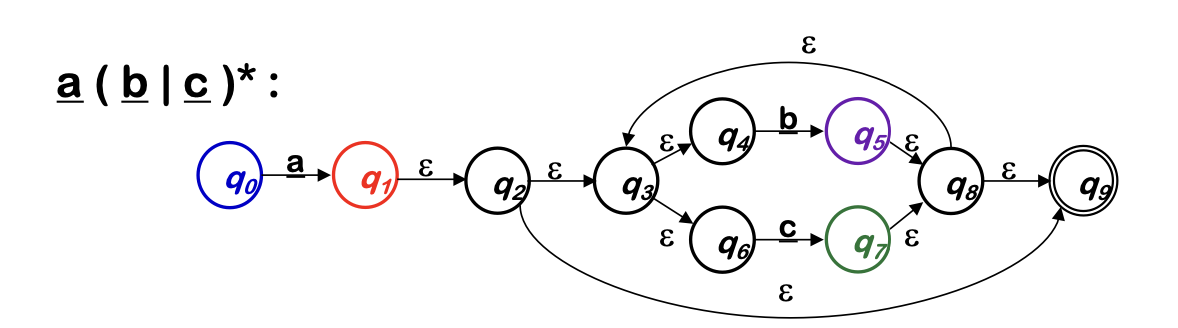
Applying the subset construction
| a | b | c | |
|---|---|---|---|
| {q0} | {q1, q2 q3, q9, q4, q6 } | none | none |
| {q1,q2,q3,q9,q4,q6} | none | {q5, q8, q3, q6, q4, q9} |
Finished in the next lecture…