Parsing (Syntax Analysis)
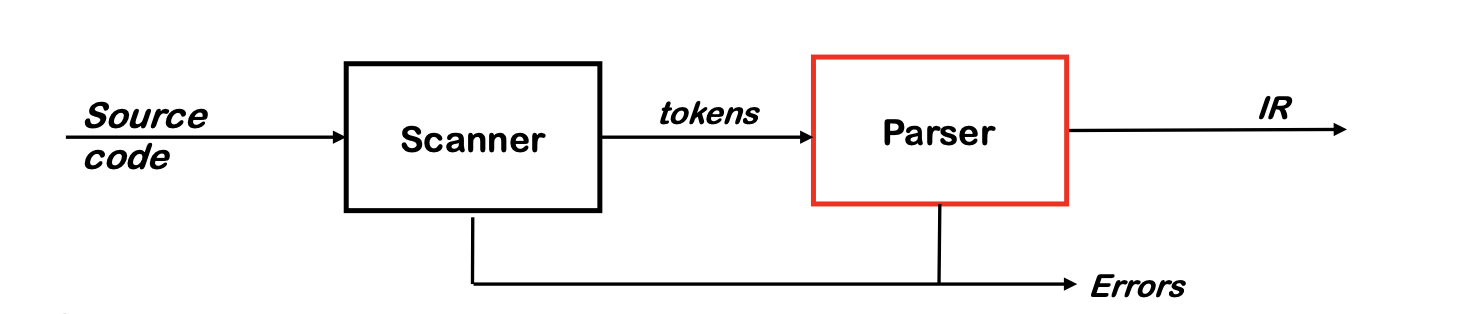
Parser
- Checks the stream of words and their parts of speech (produced by the scanner) for grammatical correctness
- Determines if input is syntactically well-formed
- Guides checking at deeper levels than syntax
- Builds an IR representation of the code
The Study of Parsing
The process of discovering a derivation for some sentence
- Need a mathematical model of syntax - a grammar G
- Need an algorithm for testing membership in L(G)
- Need to keep in mind that our goal is building parsers, not studying the mathematics of arbitrary languages
Roadmap
- Context-free grammars and derivations
- Top-down parsing
- LL(1) parsers, hand-coded recursive descent parsers
- Bottom-up parsing
- Automatically generated LR(1) parsers
Specifying Syntax with a Grammar
Context-free syntax is specified with a context-free grammar
SheepNoise -> SheepNoise baa
| baaThis CFG defines the set of noises sheep normally make
It is written in a variant of Backus-Naur form
Formally, a grammar is a four tuple, G = (S, N, T, P), where
- S is the start symbol (set of strings in L(G))
- N is the set of non-terminal symbols (syntactic variables)
- T is a set of terminal symbols (words or tokens)
- P is a set of productions or rewrite rules (P: N -> N ∪ T)*)
L(G) = { w ∈ T* | S =>* w }
A Simple Expression Grammar
To explore the uses of CFGs, we need a more complex grammar G
Expr -> Expr Op Expr
| number
| id
Op -> +
| -
| \*
| /- Such a sequence of rewrites is called a derivation
- Process of discovering a derivation is called parsing
Is x - 2 \* y ∈ L(G)?
| Rule | Sentential Form |
|---|---|
| - | Expr |
| 1 | Expr Op Expr |
| 3 | <id,x> Op Expr |
| 5 | <id,x> - Expr |
| 1 | <id,x> - Expr Op Expr |
| 2 | <id,x> - <num,2> Op Expr |
| 6 | <id,x> - <num,2> * Expr |
| 3 | <id,x> - <num,2> * <id,y> |
Derivations
- At each step, we choose a non-terminal to replace
- Different choices can lead to different derivations
Two derivations are of interest
- Leftmost derivation - replace the leftmost NT at each step
- Generates left sequential forms (=>*lm)
- Rightmost derivation - replace the rightmost NT at each step
- Generates right sequential forms (=>*rm)
These are the two systematic derivations
- We don’t care about randomly-ordered derivations!
The example above was a leftmost derivation
- Of course, there is also a rightmost derivation
- Interestingly, the resulting parse trees may be different
Parse Trees
Rule in our grammar: Expr -> Expr Op Expr
A single derivation step ... Expr ... => ... Expr Op Expr ... can be represented as a tree structure with the left-hand side non-terminal as the root, and all right-hand side symbols as the children (ordered left to right)
The entire derivation of a sentence in the language can be represented as a parse tree with the start symbol as its root, and leave nodes that are all terminal symbols
NOTE: the structure of the parse tree has semantic significance
Two derivations for x - 2 * y
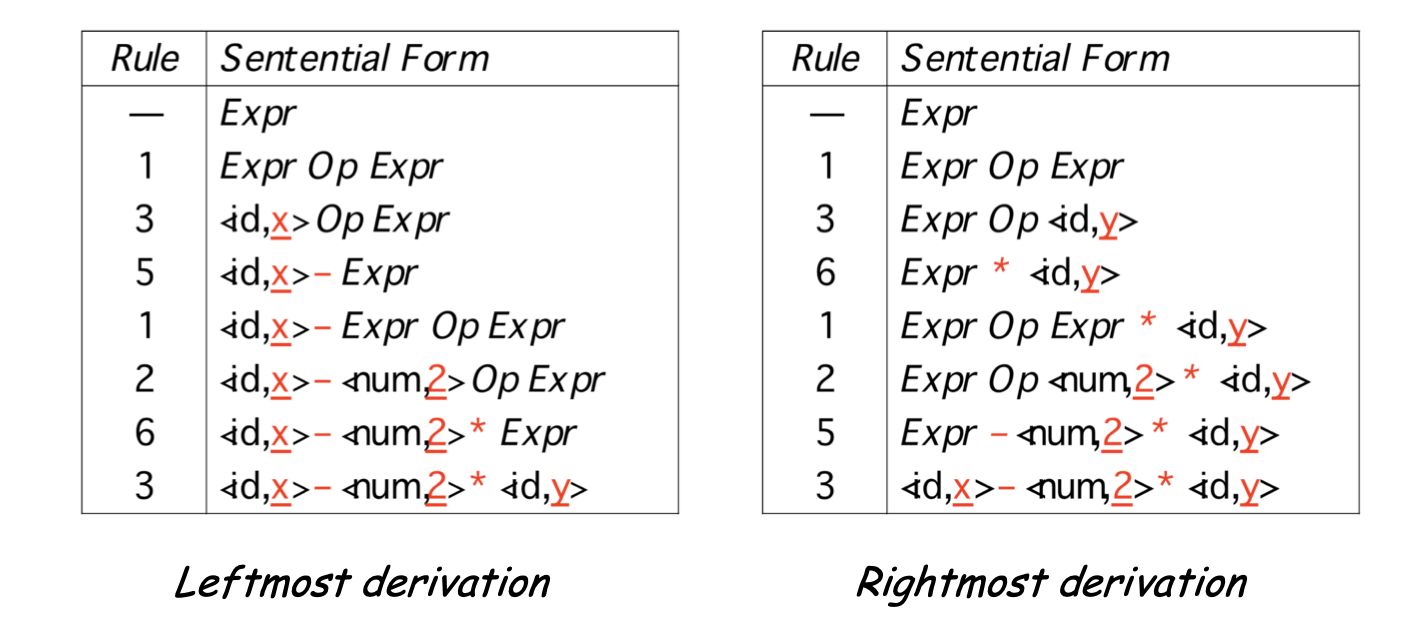
In both cases, Expr =>* id - num * id
- The two derivations produce different parse trees
- The parse trees imply different evaluation orders!
Derivations and Precedence
These two derivations point out a problem with the grammar. How to resolve ambiguity? Answer: Change grammar to enforce operator precendence and associativity
To add precedence
- Create a non-terminal for each level of precendence
- Isolate the corresponding part of the grammar
- Force the parser to recognize high precendence subexpressions first
For algebraic expressions
- Multiplication and division, first (level one)
- Subtraction and addition, next (level two)
Note: we are ignoring the issue of associativity for now
Adding the standard algebraic precendence produces:
Goal -> Expr
Expr -> Expr + Term
| Expr - Term
| Term
Term -> Term * Factor
| Term / Factor
| Factor
Factor -> number
| idThe grammar is slightly larger
- Takes more rewriting to reach some terminal symbols
- Encodes expected precedence
- Produces same parse tree under leftmost & rightmost derivations
Let’s see how it parses x - 2 * y
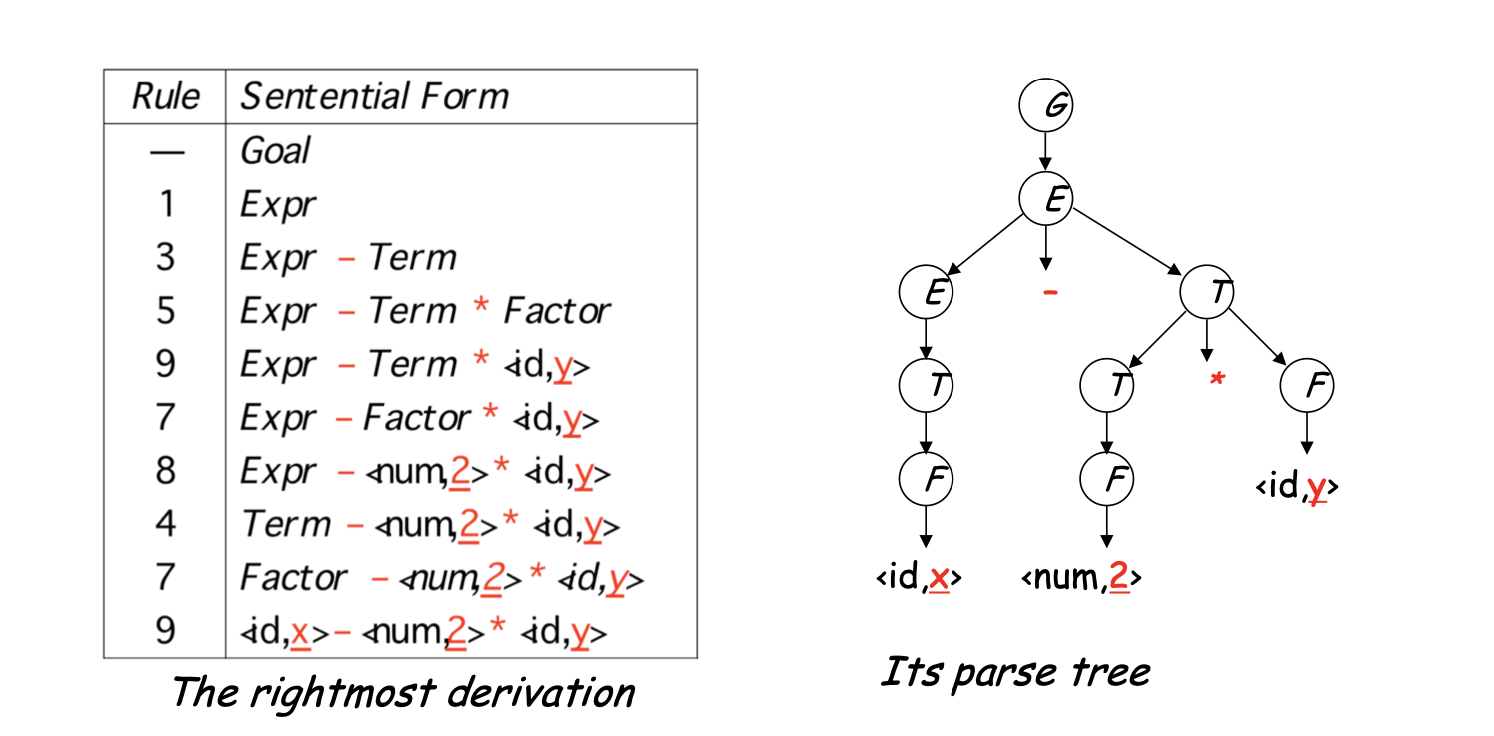
This produces x - (2 * y), along with an appropriate parse tree.
Both the leftmost and rightmost derivations give the same expression, because the grammar directly encodes the desired precedence.
Ambiguous Grammars
Definitions
- If a grammar has more than one leftmost derivation for a single sentential form, the grammar is ambiguous
- If a grammar has more than one rightmost derivation for a single sentential form, the grammar is ambiguous
- The leftmost and rightmost derivations for a sentential form may differ, even in an unambiguous grammar
Classic example - the if-then-else problem
Stmt -> if Expr then Stmt
| if Expr then Stmt else Stmt
| ... other stmts ...This ambiguity is entirely grammatical in nature
This sequential form has two derivations
if Expr then if Expr then Stmt else Stmt
if Expr then
if Expr then Stmt
else StmtOR
if Expr then
if Stmt then Stmt
else StmtRemoving the Ambiguity
- We must rewrite the grammar to avoid generating the problem
- Match each else to innermost unmatched if (common sense rule)
Stmt -> WithElse
| NoElse
WithElse -> if Expr then WithElse else WithElse
| OtherStmt
NoElse -> if Expr then Stmt
| if Expr then WithElse else NoElseDeeper Ambiguity
Ambiguity usually refers to confusion in the CFG
Overloading can create a deeper ambiguity
a = f(17)- In many Algol-like languages, f could either be a function or a subscripted variable
Disambiguing this one requires context
- Really an issue of type, not context-free syntax
- Requires extra-grammatical solution (not in CFG)
- Must handle these with a different mechanism
- Step outside grammar rather than use a more complex grammar
Final Word
Ambiguity arises from two distinct sources
- Confusion in the context-free syntax
- Confusion that requires context to resolve
Resolving ambiguity
- To remove context-free ambiguity, rewrite the grammar
- Change language (e.g.: if … endif)
- To handle context-sensitive ambiguity takes cooperation
- Knowledge of declarations, types, …
- Accept a superset of L(G) & check it by other means
- This is a language design problem
Sometimes, the compiler writer accepts an ambiguous grammar
- Parsing techniques that “do the right thing”
- i.e., always select the same derivation
Parsing Techniques
Top-down Parsers
LL(1), recursive descent
- Input: read left-to-right
- Construction leftmost derivation (forwards)
- 1 input symbol look ahead
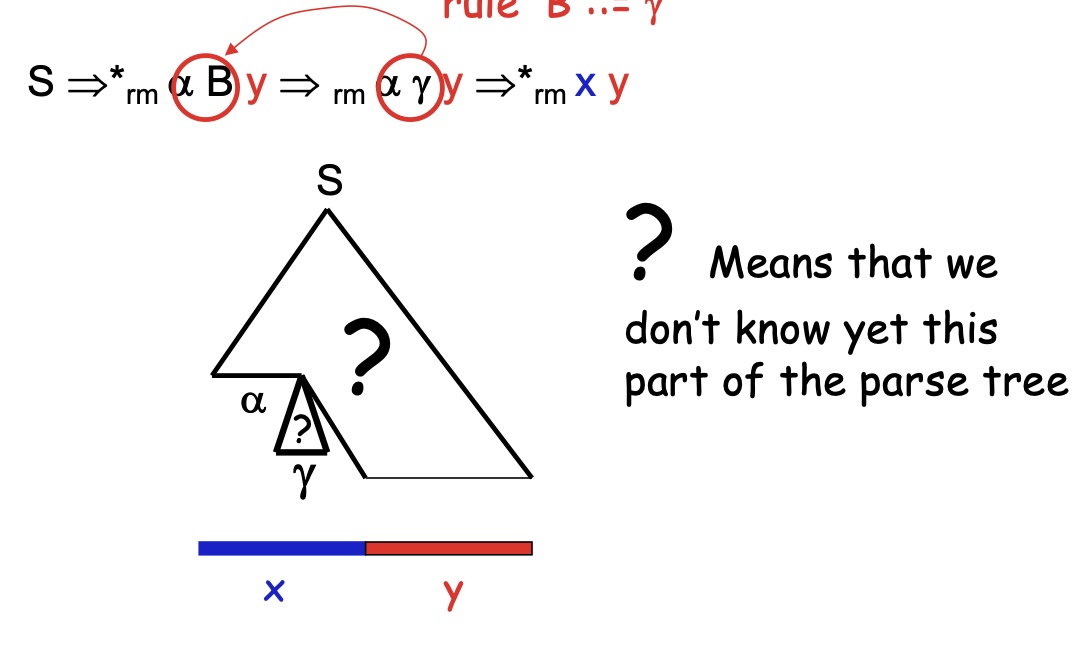
Bottom-up parsers
LR(1), operator precedence
- Input: read left-to-right
- Construct rightmost derivation (backwards)
- 1 input symbol look ahead
Comparing them both

