Lecture 9
Parser
The Big Picture
- Language syntax is specified over parts of speech (tokens)
- Syntax checking matches sequence of tokens against a grammar
- Here is an example of context free grammar (CFG) G.
1. goal -> expr
2. expr -> expr op term
3. | term
4. term -> number
5. | id
6. op -> +
7. | -G in BNF form
Math form:
S = goal
T = { number, id, +, - }
N = { goal, expr, term, op }
P = { 1, 2, 3, 4, 5, 6, 7 }Scanner - Big Picture
Why study lexical analysis?
- We want to avoid writing scanners by hand
Goals:
- To simplify specification & implementation of scanners
- To understand the underlying techniques and technologies
Regular Expressions
- Σ = {a, b, c}
- Alphabet, finite set of symbols
Syntax vs. Semantics
| Syntax - Regular Expressions | Semantics |
|---|---|
| ϵ | { ϵ } |
| a | { a } |
| --- | — |
| r1r2 | { w1, w2 | w1 ∈ L(r1), w2 ∈ L(r2) } |
| r1 | r2 | {w | w ∈ L(r1) or w ∈ L(r2) } |
| r* | ∪(i =0, ∞) Li(r) |
| r2+ | ∪(i =1, ∞) Li(r) |
Example 1
a(b|c)
a = { a } b = { b } c = { c } b | c = { b, c } a ( b | c ) = { ab, ac }
The Point
Regular expressions can be used to specify words to be translated to parts of speech (tokens) by a lexical analyzer
Using results from automata theory and theory algorithms, we can automatically build recognizers from regular expressions
=> We study REs and associated theory to automate scanner construction!
Example 2
Consider the problem of recognizing ILOC register names
Register -> r (0|1|2|...|9) (0|1|2|...|9)*
- Allows registers of arbitrary number
- Requires at least one digit
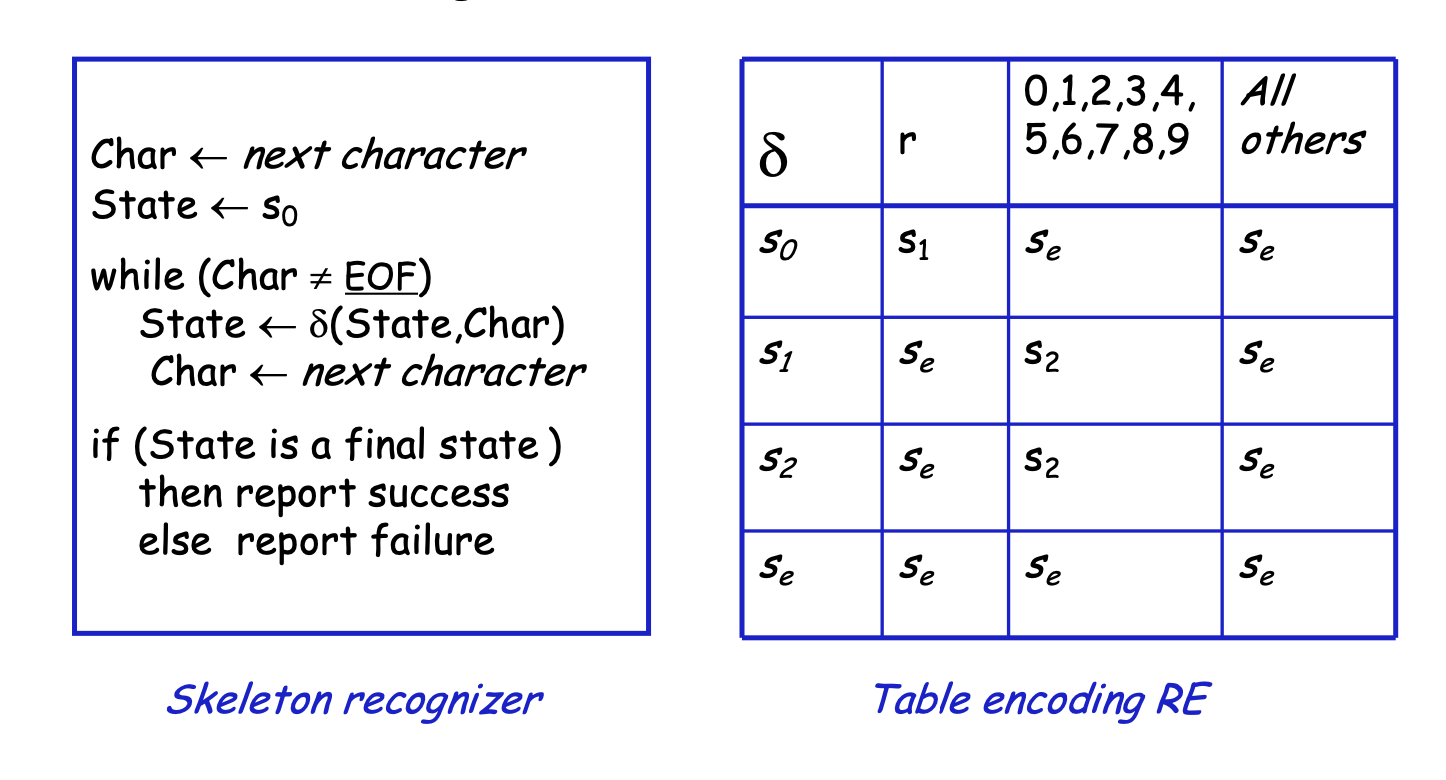
RE corresponds to a recognizer (or DFA)
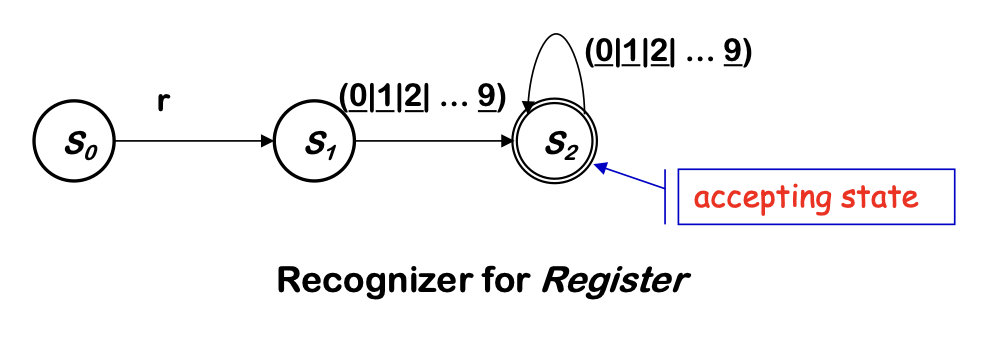
DFA Operation
- Start in state s0 & take transitions on each input character
- DFA accepts a word x if and only if x leaves it in a final state (s2)
So,
- r17 takes it through s0, s1, s2 and accepts
- r takes it through s0, s1, and fails
- a takes it straight to error state se (not shown here)
To be useful, recognizer must turn into code