Lecture 14

FIRST Set

To build FIRST(𝛂) for 𝛂 = X1, X2, …, Xn:

1. a ∈ FIRST(𝛂) if a ∈ FIRST(Xi) and 𝛆 ∈ FIRST(Xj) for all 1 <= j <= i

2. 𝛆 ∈ FIRST(𝛂) if 𝛆 ∈ FIRST(Xi) for all 1 <= i <= n

FOLLOW Set

For a non-terminal A, define FOLLOW(A) as the set of terminals that can appear immediately to the right of A in some sentential form

Thus, a non-terminal’s FOLLOW set specifies the tokens that can legally appear after it; a terminal has no FOLLOW set

FOLLOW(A) = { a ∈ (T ∪ {eof})| S eof =>* 𝛂 A a 𝛄 }

To build FOLLOW(X) for all non-terminal X:

1. Place eof in FOLLOW()

• iterate until no more terminals or eof can be added to any FOLLOW(X):

2. If A -> 𝛂B𝛃 then

• put {FIRST(𝛃) - 𝛆} in FOLLOW(B)

3. If A -> 𝛂B then

• put FOLLOW(A) in FOLLOW(B)

4. If A -> 𝛂B𝛃 and 𝛆 ∈ FIRST(𝛃) then

• put FOLLOW(A) in FOLLOW(B)

Predictive Parsing

If A -> 𝛂 and A -> 𝛃 and 𝛆 ∈ FIRST(𝛂), then we need to ensure that FIRST(𝛃) is disjoint from FOLLOW(A), too

This means that we need to update our LL(1) property to be:

A grammar is LL(1) iff A -> 𝛂 and A -> 𝛃 implies FIRST+(𝛂) ∩ FIRST+(𝛃) = ∅

• Notice we use FIRST+ instead of FIRST, in order to deal with 𝛆

This would allow the parser to make a correct choice with a look ahead of exactly one symbol!

Building Top Down Parsers

Building the complete table

• Need a row for every NT & a column for every T + “eof”
• Need an algorithm to build the table

Filling in TABLE[X,y], X ∈ NT, y ∈ T ∪ { eof }

• entry is the rule X -> 𝛃, if y ∈ FIRST+(𝛃)
• entry is error otherwise

If any entry is defined multiple times, G is not LL(1)

LL(1) Skeleton Parser

token = next_token() // scanner call
psuh EOF onto Stack
push the start symbol, S, onto Stack
TOS = top of Stack

loop forever
  if TOS = EOF and token = EOF then
    break and report success
  else if TOS is a terminal token then
    if TOS matches token then
      pop Stack  // recognized TOS
      token = next_token()
    else report error looking for TOS
  else  // TOS is a non-terminal symbol
    if TABLE[TOS, token] is A -> B1,B2,...,Bk then
      pop Stack // get rid of A
      push Bk,Bk-1,...,B1 // in that order
    else report error expanding TOS
  TOS = top of Stack

LL(1) Parser Example

Table-drive LL(1) parser

How to parse input aaabbb? Describe action as sequence of states (PDA stack content, remaining input, next action), use eof as bottom-of-stack marker

PDA stack content: [X, … Z], where Z is the TOS next actions: rule or next input + pop or error or accept

Recursive descent LL(1) parser

1. Every NT is associated with a parsing procedure
2. The parsing procedure for A ∈ NT, proc A, is responsible to parse and consume any (token) string that can be derived from A; it may recursively call other parsing procedures
3. The parser is invoked by calling proc S for start symbol S

Reminder: Left Recursion

Top-down parsers cannot handle left-recursive grammars

Our expression grammar is left recursive

• This can lead to non-termination in a top-down parser
• For a top-down parser, any recursion must be right recursion
• We would like to convert the left recursion to right recursion

Left Factoring

What if my grammar does not have the LL(1) property? => Sometimes, we can transform the grammar

The algorithm

A graphical example:

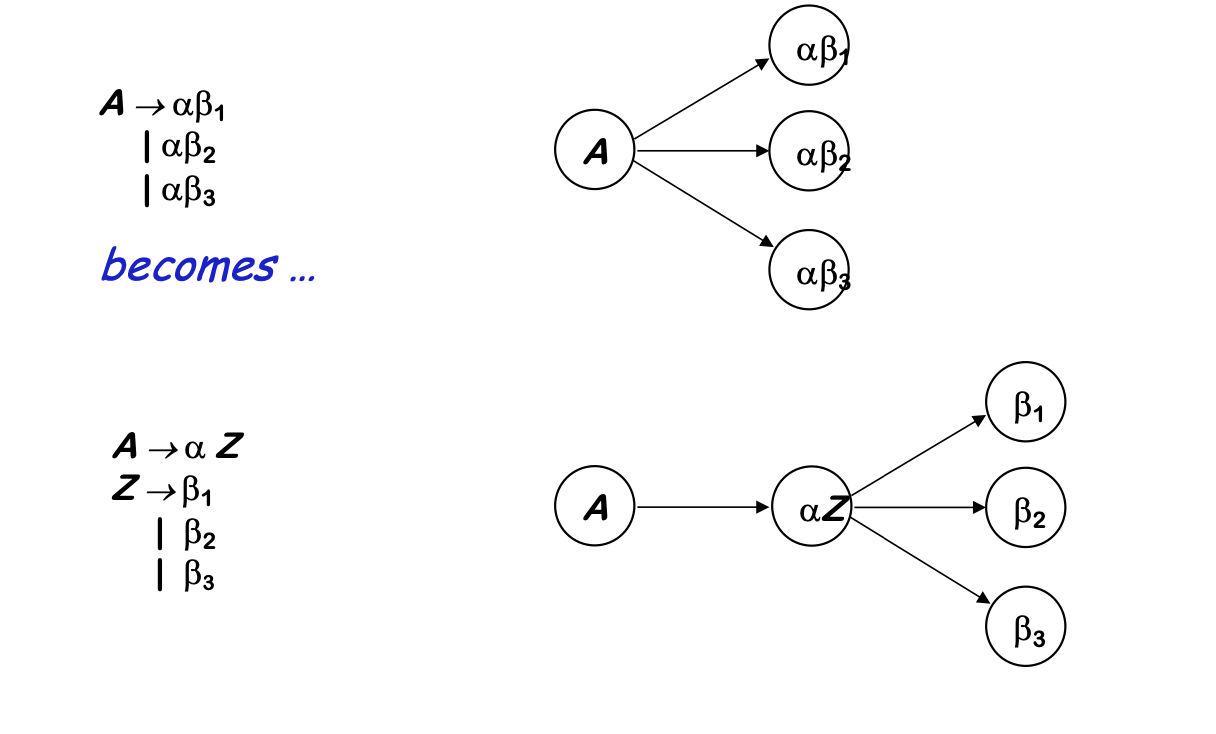
Consider the following fragment of the expression grammar

Factor  -> Identifier
         | Identifier [ExprList]
         | Identifier (ExprList)

After left factoring, it becomes

Factor    -> Identifier Arguments
Arguments -> [ExprList]
          -> (ExprList)
          -> 𝛆

This form has the same syntax, with the LL(1) property

LL(1) Grammars

Question: By eliminating left recursion and left factoring, can we transform an arbitrary CFG to a form where it meets the LL(1) condition? (and can be parsed predictively with single token look ahead?)

Answer: Given a CFG that doesn’t meet the LL(1) condition, it is undecidable whether or not an equivalent LL(1) grammar exists.