Lecture 16 - Bottom-up Parsing

LR(1) Skeleton Parser

stack.push(INVALID); stack.push(s0);
not_found = true;
token = scanner.next_token();
do while (not_found) {
  s = stack.top();
  if (ACTION[s, token] == "reduce A -> 𝝱") {
    stack.popnum(2 * |𝝱|);
    s = stack.top();
    stack.push(A);
    stack.push(GOTO[s, A]);
  } else if (ACTION[s, token] == "shift si") {
    stack.push(token);
    stack.push(si);
    token <- scanner.next_token();
  } else if (ACTION[s, token] == "accept" && token == EOF) {
    not_found = false;
  } else {
    report a syntax error and recover;
  }
}

report success

The skeleton parser:

Uses ACTION & GOTO tables
Does |words| shifts
Does |derivation| reductions
Does 1 accept

Building LR(1) Parsers

How do we generate the ACTION and GOTO tables?

Use the grammar to build a model of the DFA
Use the model to build ACTION and GOTO tables
If construction succeeds, the grammar is LR(1)

The Big Picture:

Model the state of the parser
Use two functions goto(s, X) and closure(s)
- goto() is analagous to move() in subset construction
- closure() adds information to round out a state
Build up states and transition functions of the DFA
Use the information to fill in the ACTION and GOTO tables

LR(k) items

The LR(1) table construction algorithm uses LR(1) items to represent valid configurations of an LR(1) parser

An LR(k) item is a pair [P, x] where

P is a production A -> 𝝱 with a . at some position in the rhs
x is a look ahead string of length <= k
The . in an item indicates the position in the top of the stack

LR(1):

[A -> .𝝱𝝲, a] means that the input seen so far is consistent with the use of A -> 𝝱𝝲 immediately after the symbol on the top of the stack
[A -> 𝝱.𝝲, a] means that the input seen so far is consistent with the use of A -> 𝝱𝝲 at this point in the parse, and that the parser has already recognized 𝝱
[A -> 𝝱𝝲., a] means that the parser has seen 𝝱𝝲, and that a look ahead symbol of a is consistent with reducing to A.

LR(1) items

The production A -> 𝝱, where 𝝱 = B1B2B3 with look ahead a, can give rise to 4 items

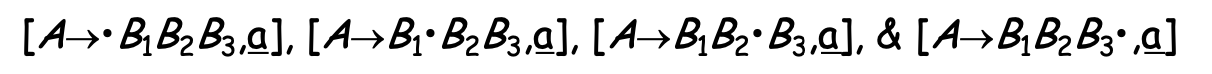
The set of LR(1) items for a grammar is finite

What’s the point of all these look ahead symbols?

Carry them along to choose the correct reduction, if there is a choice
Look ahead’s are bookkeeping, unless item has a · at the right end
- Has no direct use in [A -> 𝝱·𝝲]
- In [A -> 𝝱·, a], a look ahead of a implies a reduction by A -> 𝝱
- For { [A -> 𝝱·, a], [B -> 𝝲·c, b] }, a => reduce to A; c => shift
Limited right context is enough to pick the choices (unique, i.e., deterministic choice)

LR(1) Table Construction

High level overview

Build the canonical collection of sets of LR(1) Items, I

Begin in an appropriate state, s0
- Assume S’ -> S, and S’ is unique start symbol that does not occur on any RHS of a production
- [S’ -> ·S, EOF] along with any equivalent items
- Derive equivalent items as closure(s0)
Repeatedly compute, for each sk, and each X, goto(sk, X)
- If the set is not already in the collection, add it
- Record all the transitions created by goto()
- This eventually reaches a fixed point

Fill in the table from the collection of sets of LR(1) items

The canonical collection completely encodes the transition diagram for the handle-finding DFA

Computing Closures

closure(s) adds all the items implied by items already in s

Any item [A -> 𝝱·Bφ, a] implies [B -> ·𝛕, x] for each production with B on the lhs, and each x ∈FIRST(φa)

Computing Gotos

goto(s,x) computes the state that the parser would reach if it recognized an X while in state s

Goto({ [A -> 𝝱·Xφ, a]}, X) produces [A -> 𝝱X·φ, a] (easy part)
Should also include closure([A -> 𝝱X·φ, a])

Building the Canonical Collection

Start from s0 = closure([S’ -> S, EOF])
Repeatedly construct new states, until all are found