Lecture 13 - More Parsing

Top-down parsers

LL(1), recursive descent

• Input: read left to right
• Construct leftmost derivation
• 1 input symbol look ahead

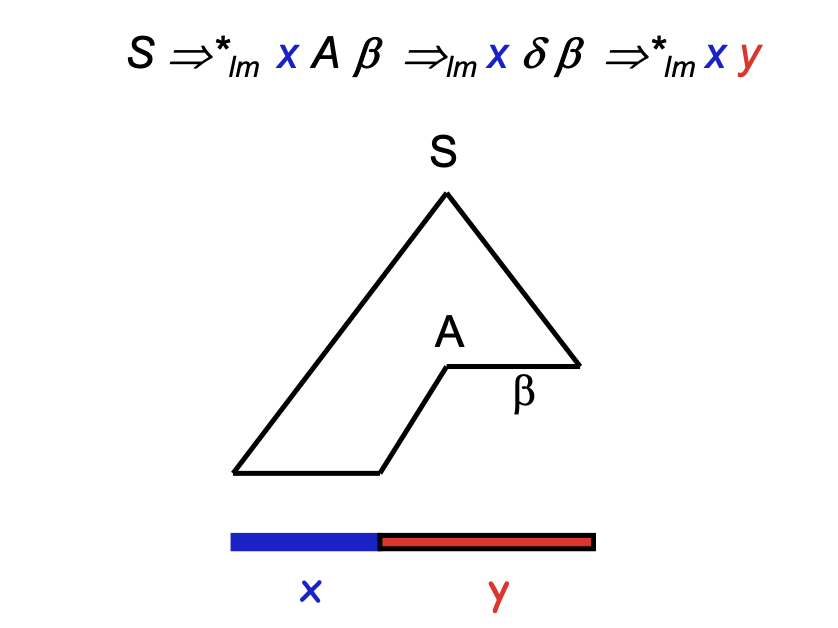
Example

Grammar S -> % S % | & S & | $

Our language can be described mathematically as: {w $ w^R | w ∈ (%, &)^*}

Is this LL(1)?

Yes! Because as you push the left most derivation through, you only need to look ahead one token at a time, and you end up with a deterministic parse tree.

The grammar S -> % S % | % & S % | $ is NOT LL(1), but rather LL(2).

Formally defining LL(1)

A -> 𝝰 | 𝛃 s.t. First(𝝰) ∩ First(𝛃) = ∅

But, how do we compute the First sets?

Left Recursion

Remember the expression grammar?

Goal    -> Expr
Expr    -> Expr + Term
        |  Expr - Term
        |  Term
Term    -> Term * Factor
        | Term / Factor
        | Factor
Factor  -> number
        | id

Top-down parsers cannot handle left-recursive grammars

Formally, A grammar is left recursive if ∃ A ∈ NT such that ∃ a derivation A =>^+ A𝝰, for some string 𝝰 ∈ (NT ∪ T)^+

Our expression grammar is left recursive

• This can lead to non-termination in a top-down parser
• For a top-down parser, any recursion must be right recursion
• We would like to convert the left recursion to right recursion

Non-termination is a bad property in any part of a compiler

Eliminating Left Recursion

To remove left recursion, we can transform the grammar

Consider a grammar fragment of the form

Fee -> Fee 𝝰
     | 𝝱

where neither 𝝰 nor 𝝱 start with Fee

We can rewrite this as

Fee -> 𝝱 Fie
Fie -> 𝝰 Fie
     | 𝝴

where Fie is a new non-terminal

This accepts the same language, but uses only right recursion

Roadmap (Where are we?)

We set out to study parsing

• Specifying syntax
  • Context free grammars
  • Ambiguity
• Top-down parsers
  • Algorithm & its problem with left recursion
  • Left-recursion removal
  • Left factoring (will discuss later)
• Predictive top-down parsing
  • The LL(1) condition
  • Table-driven LL(1) parsers
  • Recursive descent parsers
    • Syntax directed translation (example)

Picking the “Right” production

If it picks the wrong production, a top-down parser may backtrack. Alternative is to look ahead in input & use context to pick correctly

How much look ahead is needed?

• In general, an arbitrarily large amount
• Use the Cocke-Younger, Kasami algorithm or Earley’s algorithm

Fortunately

• Large subclasses of CFGs can be parsed with limited look ahead
• Most programming language constructs fall in those subclasses

Among the interesting subclasses are LL(1) and LR(1) grammars

Predictive Parsing

Basic idea Given A -> 𝝰 | 𝝱, the parser should be able to choose between 𝝰 and 𝝱

FIRST Sets

• For some rhs 𝝰 ∈ G, define FIRST(𝝰) as the set of tokens that appear as the first symbol in some string that derives from 𝝰
• That is, a ∈ FIRST(𝝰) iff a =>^* a𝝲, for some 𝝲

The LL(1) property If A -> 𝝰 and A -> 𝝱 both appear in the grammar, we would like FIRST(𝝰) ∩ FIRST(𝝱) = ∅

• Note: This is almost correct, but not quite!

This would allow the parser to make a correct choice with a look ahead of exactly one symbol!

The FIRST Set - 1 Symbol Look ahead

The FOLLOW Set - 1 Symbol

For a non-terminal A, define FOLLOW(A) as

FOLLOW(A) := the set of terminals that can appear immediately to the right of A in some sentential form

Thus, a non-terminal’s FOLLOW set specifies the tokens that can legally appear after it; a terminal has no FOLLOW set

FOLLOW(A) = { a ∈ (T ∪ {eof}) | S eof =>^* 𝝰 A a 𝝲 }

To build FOLLOW(X) for all non-terminal X

1. Place eof in FOLLOW(<goal>)

• Iterate until no more terminals or eof can be added to any FOLLOW(X)

2. If A -> 𝝰B𝝱 then put {FIRST(𝝱) - 𝝴} in FOLLOW(B)
3. If A -> 𝝰B then put FOLLOW(A) in FOLLOW(B)
4. If A -> 𝝰B𝝱 and 𝝴 ∈ FIRST(𝝱) then put FOLLOW(A) in FOLLOW(B)

If A -> 𝝰 and A -> 𝝱 and 𝝴 ∈ FIRST(𝝰), then we need to ensure that FIRST(𝝱) is disjoint from FOLLOW(A), too