Lecture 15 - Bottom-up Parsing

Bottom-up parsers

LR(1), operator precedence

L => Input: read left-to-right
R => Construct rightmost derivation
(1) => 1 input symbol look ahead

LR(1) Parser Example

Is the following grammar LL(1), LL(2), or LR(1)?

S ::= a b | a b c

Is the following grammar LR(1) or even LR(0)?

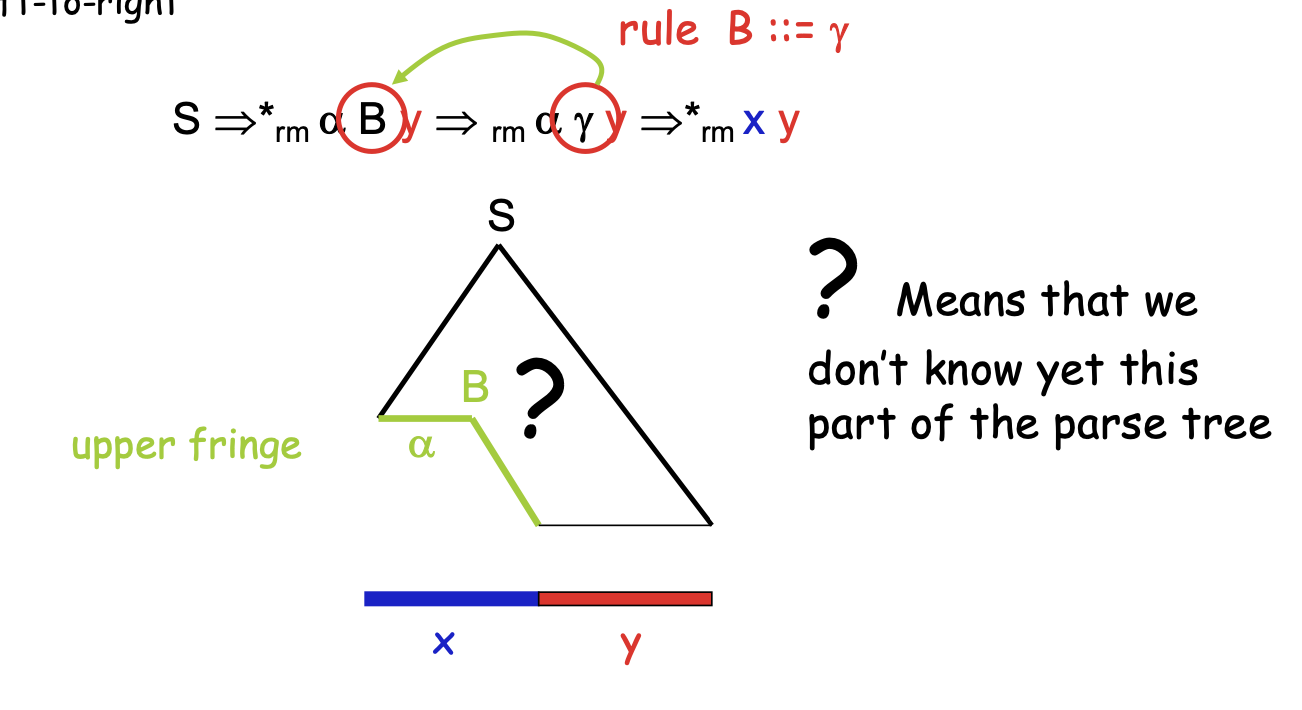
S ::= a S b | c

Basic idea:

shift symbols from input onto the stack until top of the stack is a RHS of a rule; if so, “apply” rule backwards (reduce) by replacing top of the stack by the LHS non-terminal.

Challenge: when to shift, and when to reduce.

Example 1

S' -> S
S -> a S b
S -> c

Input: aaacbbb

We can describe our states as:

State	Value
s0	[S’ -> .S], [S -> .aSb], [S -> .c]
s1	[S -> a.Sb], [S -> .aSb], [S -> .c]
s2	[S -> aS.b]
s3	[S -> aSb.]
s4	[S -> c.]
accept	[S’ -> S.]

Our transition table can be the following:

State	a	S	b	c
s0	s1	accept		s4
s1	s1	s2		s4
s2			s3
s3
s4
accept

This is actually a LR(0) grammar if we can prove we don’t need to look ahead at all!

But, when do we shift or reduce? Let’s build an action table

State	Action
s0	shift
s1	shift
s2	shift
s3	reduce
s4	reduce

We can now try to parse aaacbbb eof

Step	Input Read	Stack
0	eof	[eof, s0]
1	a	[eof, s0, a, s1]
2	a	[eof, s0, a, s1, a, s1]
3	a	[eof, s0, a, s1, a, s1, a, s1]
4	c	[eof, s0, a, s1, a, s1, a, s1, c, s4]
		[eof, s0, a, s1, a, s1, a, s1, S, s4]
5	b	[eof, s0, a, s1, a, s1, a, s1, S, s4, b, s3]
…