NFA -> DFA with Subset Construction
Need to build a simulation of the NFA
Two key functions
move(si, a)is a set of states reachable from si by aε-closure(si)is the set of states reachable from si by ε
The algorithm (sketch):
- Start state derived from s0 of the NFA
- Take its
ε-closureS0 =ε-closure(s0) - For each state S, compute
move(S, a)for each a ∈ Σ, and take it’s ε-closure - Iterate until no more states are added
Sounds more complex that it is…
Example
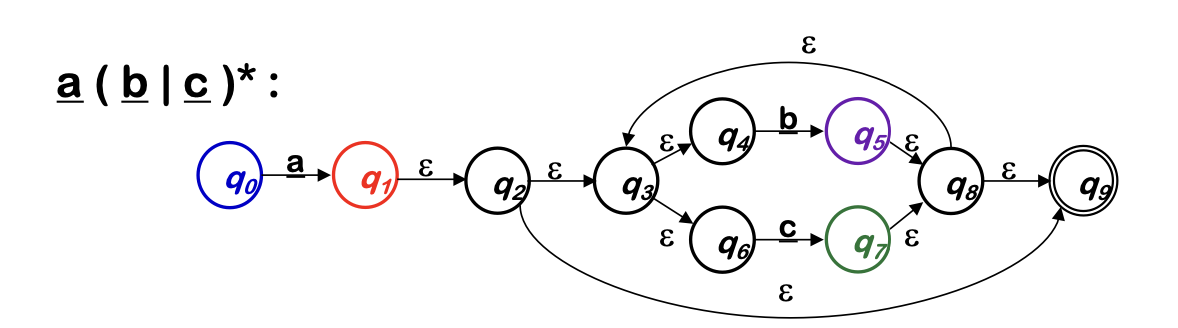
Applying the subset construction:
| DFA States | NFA States | a | b | c |
|---|---|---|---|---|
| s0 | {q0} | {q1, q2 q3, q9, q4, q6 } | none | none |
| s1 | {q1,q2,q3,q9,q4,q6} | none | {q5, q8, q3, q6, q4, q9} | {q7, q8, q9, q3, q4, q6} |
| s2 | {q5, q8, q9, q3, q4, q6 } | none | s2 | s3 |
| s3 | {q7, q8, q9, q3, q4, q6 } | none | s2 | s3 |
Note that any NFA state that contains q9 is an accepting state, since that is the final state in the NFA
The result of subset construction is the following DFA
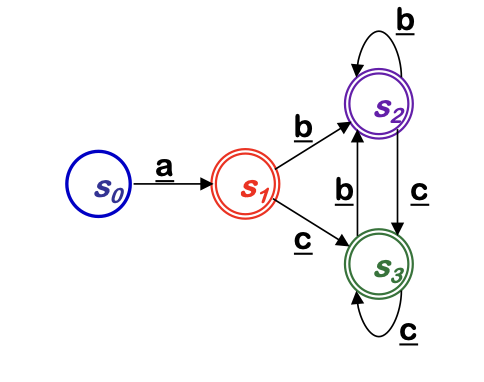
| δ | a | b | c |
|---|---|---|---|
| s0 | s1 | - | - |
| s1 | - | s2 | s3 |
| s2 | - | s2 | s3 |
| s3 | - | s2 | s3 |
- Ends up smaller than the NFA
- All transitions are deterministic
Automatic Scanner Construction
-
RE -> NFA (Thompson’s construction)
- Build an NFA for each term
- Combine them with ε moves
-
NFA -> DFA (subset construction)
- Build the simulation
-
DFA -> Minimal DFA
- Hopcroft’s Algorithm
-
DFA -> RE (not really part of scanner construction)
- All pairs, all paths problem
- Union together paths from s0 to a final state
DFA Minimization
- How do we know whether two states encode the same information?
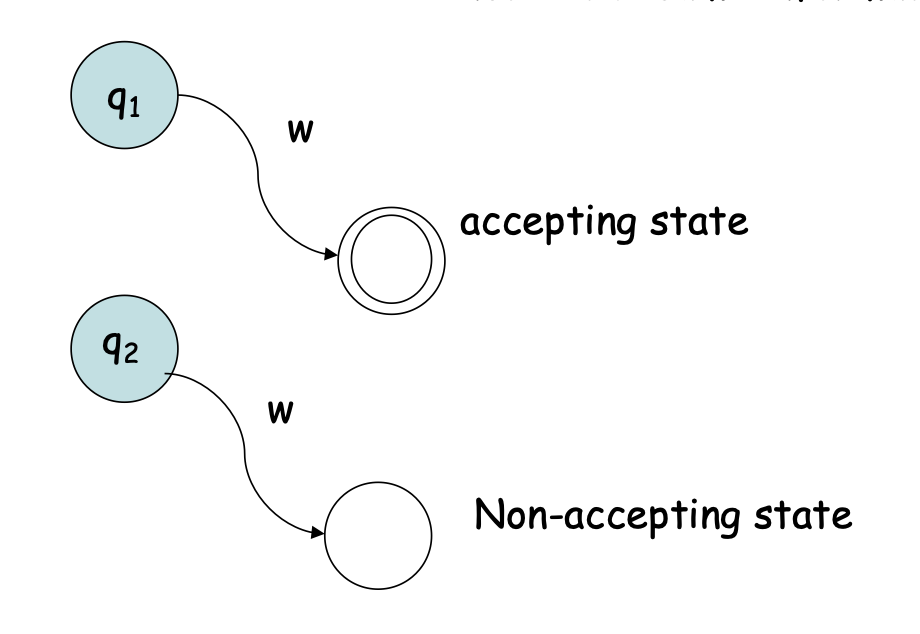
- Here, q1 and q2 are not equivalent. “w” is a witness that they are not equivalent
Intuition: Two states are equivalent if for all sequences of input symbols “w” they both lead to an accepting state, or both end up in a non-accepting state.
Big Picture
- Discover sets of equivalent states
- Represent each such set with just one state
Two states are equivalent if and only if:
- ∀ a ∈ Σ, transitions on a lead to equivalent states (DFA)
- if a-transitions to different sets => two states must be in different sets, i.e., cannot be equivalent
A partition P of S
- Each state s ∈ S is in exactly one set pi ∈ P
- The algorithm iteratively partitions the DFA’s states
Details of the algorithm
- Group states into maximal size sets, optimistically
- Iteratively subdivide those sets, as needed
- States that remain grouped together are equivalent
Initial partition, P0, has two sets: {F} & {Q-F}
Splitting a set (“partitioning a set s by a”)
- Assume qa & qb ∈ s, and δ(qa, a) = qx & δ(qb, a) = qy
- If qx & qy are not in the same set, i.e., are considered equivalent, then s must be split
- qa has transition on a, qb does not => a splits s
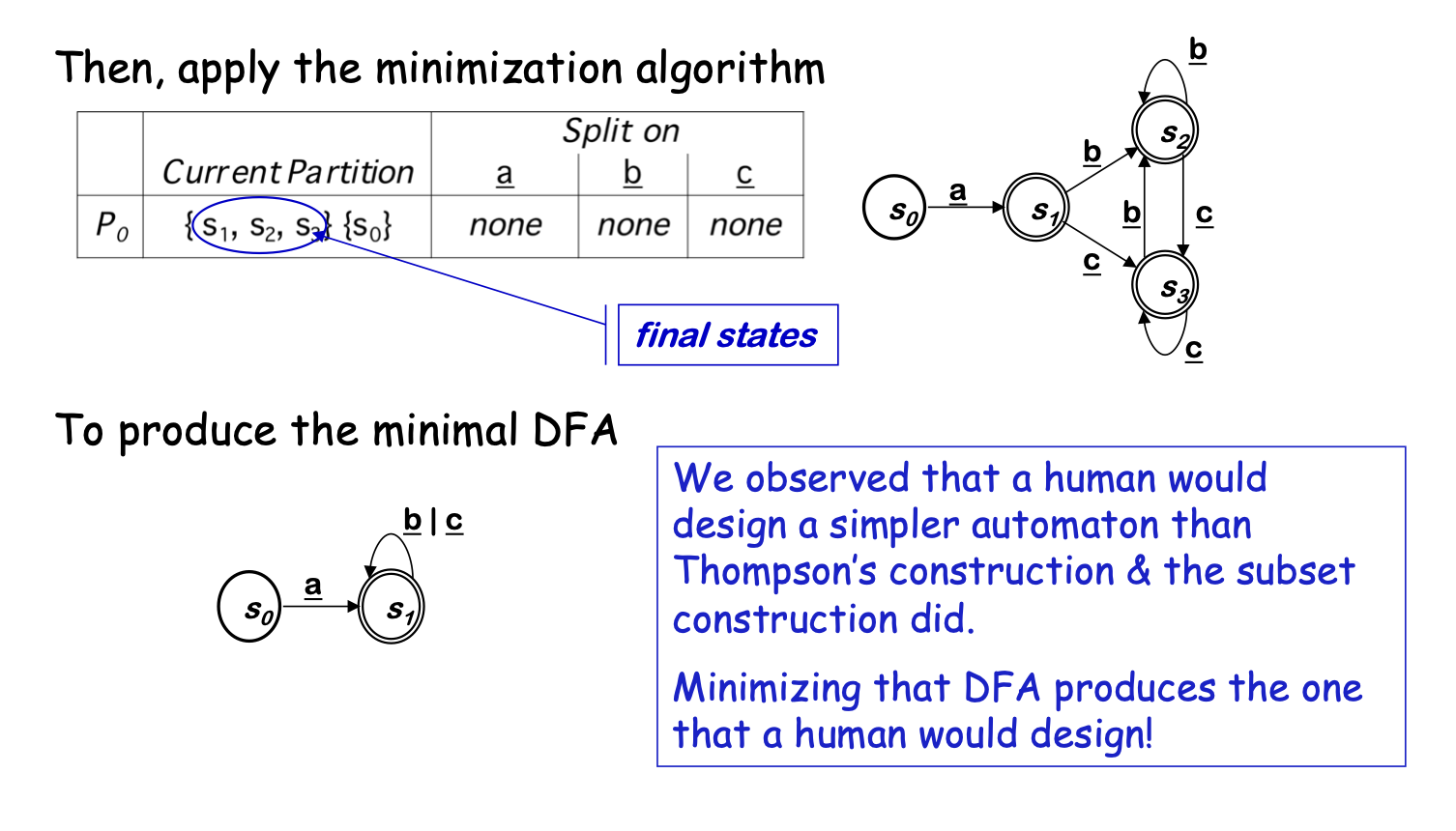
Back to our DFA Minimization example
Limits of Regular Languages
Advantages of Regular Expressions
- Simple & powerful notation for specifying patterns
- Automatic construction of fast recognizers
- Many kinds of syntax can be specified with REs
Example - an expression grammar
Term -> [a-zA-Z]([a-zA-Z] | [0-9])*
Op -> + | - | * | /
Expr -> ( Term Op )* TermOf course, this would generate a DFA
If REs are so useful… Why not use them for everything?
Not all languages are regular
RL’s ⊂ CFL’s ⊂ CSL’s
You cannot construct DFAs to recognize these languages
- L = {p^k q^k}
- L = {wcw^r | w ∈ Σ*}
Neither of these is a regular language But, this is a little subtle. You can construct DFA’s for
- Strings with alternating 0’s and 1’s
- Strings with an even number of 0’s and 1’s
- Strings of bit patterns that represent binary numbers which are divisible by 5 (homework)
What can be so hard?
Poor language design can complicate scanning
- Reserved words are important
if then then then - else; else else = then(PL/I)
- Insignificant blanks (Fortran & Algol68)
do 10 i = 1,25do 10 i = 1.25
- String constants with special characters (C, C++, Java)
- newline, tab, quote, comment delimiters
- Limited identifier “length” (Fortran 66 & PL/I)